tricontourf
Makie.tricontourf Function
tricontourf(triangles::Triangulation, zs; kwargs...)
tricontourf(xs, ys, zs; kwargs...)Plots a filled tricontour of the height information in zs at the horizontal positions xs and vertical positions ys. A Triangulation from DelaunayTriangulation.jl can also be provided instead of xs and ys for specifying the triangles, otherwise an unconstrained triangulation of xs and ys is computed.
Plot type
The plot type alias for the tricontourf function is Tricontourf.
Examples
using CairoMakie
using Random
Random.seed!(1234)
x = randn(50)
y = randn(50)
z = -sqrt.(x .^ 2 .+ y .^ 2) .+ 0.1 .* randn.()
f, ax, tr = tricontourf(x, y, z)
scatter!(x, y, color = z, strokewidth = 1, strokecolor = :black)
Colorbar(f[1, 2], tr)
f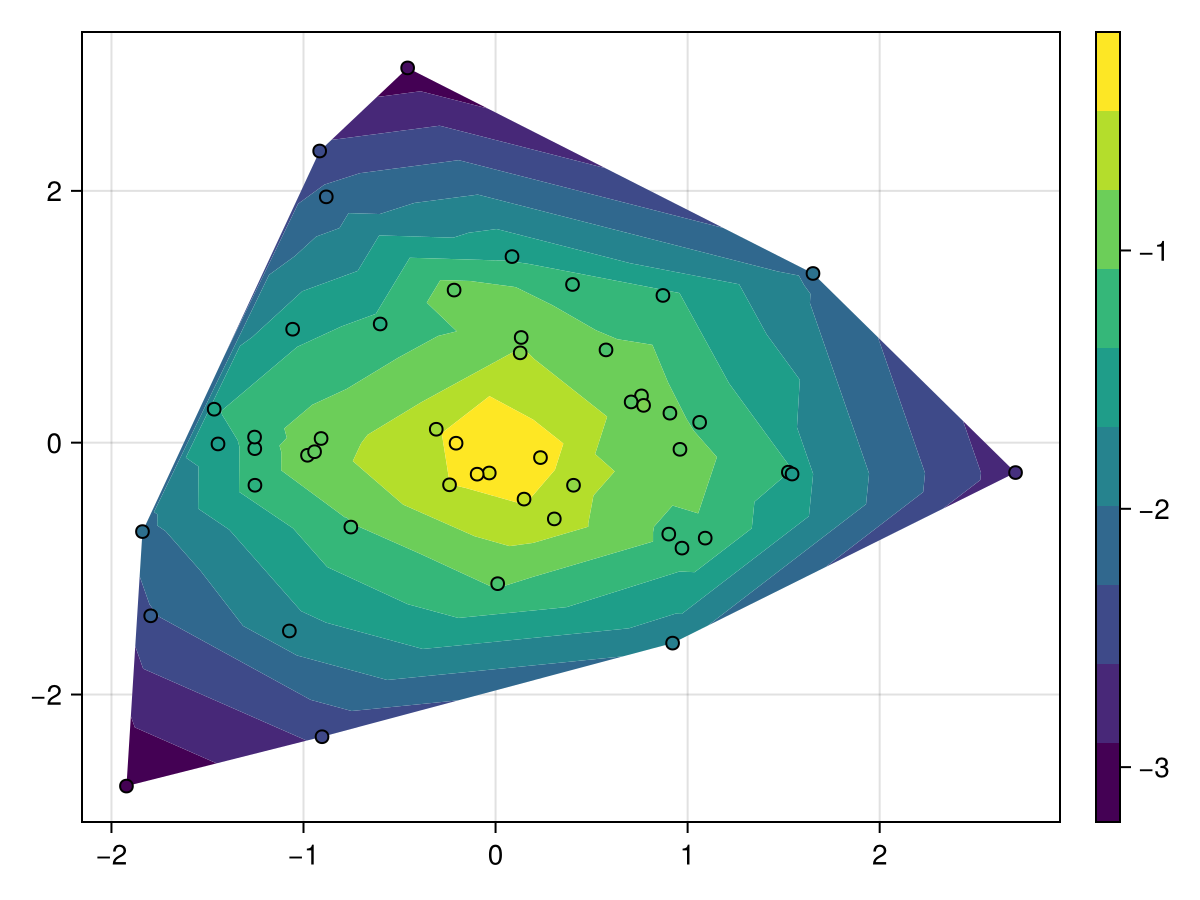
using CairoMakie
using Random
Random.seed!(1234)
x = randn(200)
y = randn(200)
z = x .* y
f, ax, tr = tricontourf(x, y, z, colormap = :batlow)
scatter!(x, y, color = z, colormap = :batlow, strokewidth = 1, strokecolor = :black)
Colorbar(f[1, 2], tr)
f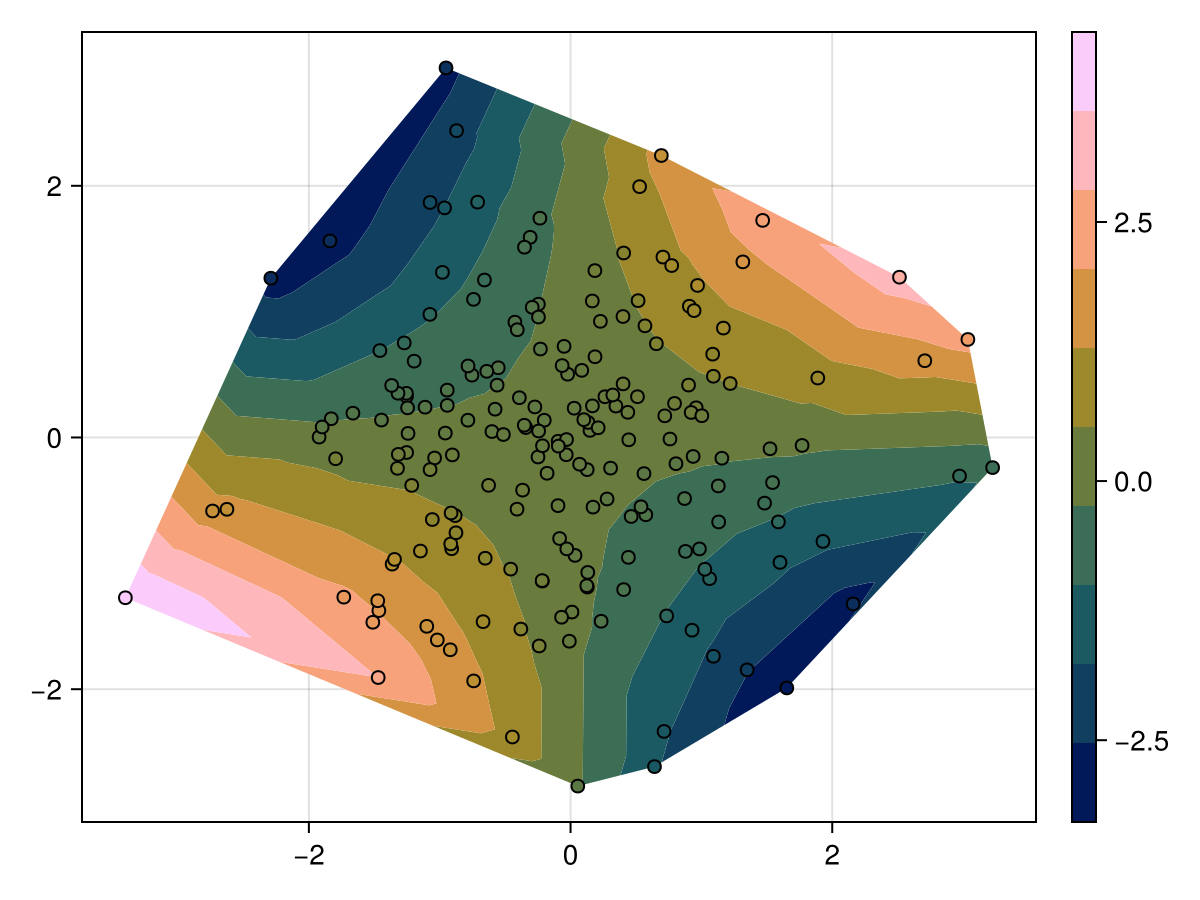
Triangulation modes
Manual triangulations can be passed as a 3xN matrix of integers, where each column of three integers specifies the indices of the corners of one triangle in the vector of points.
using CairoMakie
using Random
Random.seed!(123)
n = 20
angles = range(0, 2pi, length = n+1)[1:end-1]
x = [cos.(angles); 2 .* cos.(angles .+ pi/n)]
y = [sin.(angles); 2 .* sin.(angles .+ pi/n)]
z = (x .- 0.5).^2 + (y .- 0.5).^2 .+ 0.5.*randn.()
triangulation_inner = reduce(hcat, map(i -> [0, 1, n] .+ i, 1:n))
triangulation_outer = reduce(hcat, map(i -> [n-1, n, 0] .+ i, 1:n))
triangulation = hcat(triangulation_inner, triangulation_outer)
f, ax, _ = tricontourf(x, y, z, triangulation = triangulation,
axis = (; aspect = 1, title = "Manual triangulation"))
scatter!(x, y, color = z, strokewidth = 1, strokecolor = :black)
tricontourf(f[1, 2], x, y, z, triangulation = Makie.DelaunayTriangulation(),
axis = (; aspect = 1, title = "Delaunay triangulation"))
scatter!(x, y, color = z, strokewidth = 1, strokecolor = :black)
f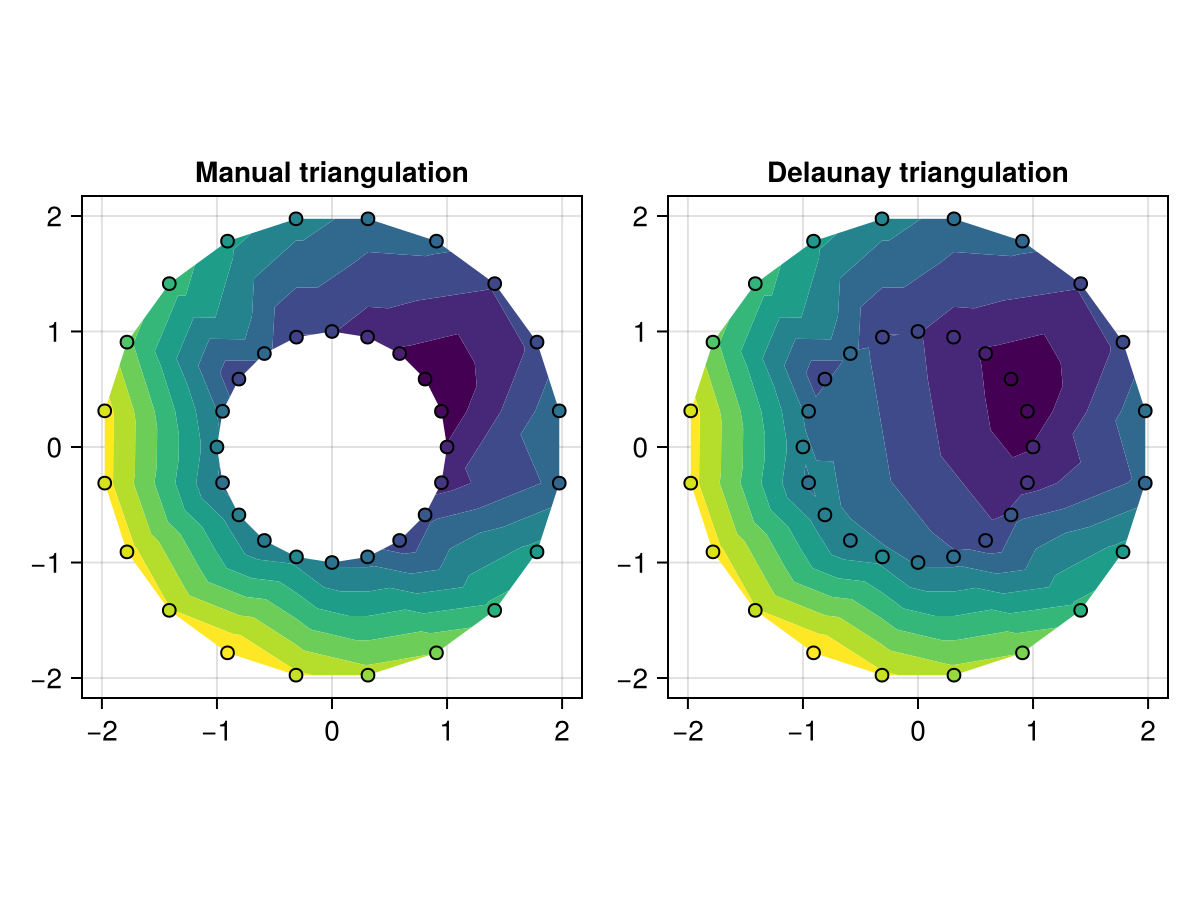
By default, tricontourf performs unconstrained triangulations. Greater control over the triangulation, such as allowing for enforced boundaries, can be achieved by using DelaunayTriangulation.jl and passing the resulting triangulation as the first argument of tricontourf. For example, the above annulus can also be plotted as follows:
using CairoMakie
using DelaunayTriangulation
using Random
Random.seed!(123)
n = 20
angles = range(0, 2pi, length = n+1)[1:end-1]
x = [cos.(angles); 2 .* cos.(angles .+ pi/n)]
y = [sin.(angles); 2 .* sin.(angles .+ pi/n)]
z = (x .- 0.5).^2 + (y .- 0.5).^2 .+ 0.5.*randn.()
inner = [n:-1:1; n] # clockwise inner
outer = [(n+1):(2n); n+1] # counter-clockwise outer
boundary_nodes = [[outer], [inner]]
points = [x'; y']
tri = triangulate(points; boundary_nodes = boundary_nodes)
f, ax, _ = tricontourf(tri, z;
axis = (; aspect = 1, title = "Constrained triangulation\nvia DelaunayTriangulation.jl"))
scatter!(x, y, color = z, strokewidth = 1, strokecolor = :black)
f
Boundary nodes make it possible to support more complicated regions, possibly with holes, than is possible by only providing points themselves.
using CairoMakie
using DelaunayTriangulation
## Start by defining the boundaries, and then convert to the appropriate interface
curve_1 = [
[(0.0, 0.0), (5.0, 0.0), (10.0, 0.0), (15.0, 0.0), (20.0, 0.0), (25.0, 0.0)],
[(25.0, 0.0), (25.0, 5.0), (25.0, 10.0), (25.0, 15.0), (25.0, 20.0), (25.0, 25.0)],
[(25.0, 25.0), (20.0, 25.0), (15.0, 25.0), (10.0, 25.0), (5.0, 25.0), (0.0, 25.0)],
[(0.0, 25.0), (0.0, 20.0), (0.0, 15.0), (0.0, 10.0), (0.0, 5.0), (0.0, 0.0)]
] # outer-most boundary: counter-clockwise
curve_2 = [
[(4.0, 6.0), (4.0, 14.0), (4.0, 20.0), (18.0, 20.0), (20.0, 20.0)],
[(20.0, 20.0), (20.0, 16.0), (20.0, 12.0), (20.0, 8.0), (20.0, 4.0)],
[(20.0, 4.0), (16.0, 4.0), (12.0, 4.0), (8.0, 4.0), (4.0, 4.0), (4.0, 6.0)]
] # inner boundary: clockwise
curve_3 = [
[(12.906, 10.912), (16.0, 12.0), (16.16, 14.46), (16.29, 17.06),
(13.13, 16.86), (8.92, 16.4), (8.8, 10.9), (12.906, 10.912)]
] # this is inside curve_2, so it's counter-clockwise
curves = [curve_1, curve_2, curve_3]
points = [
(3.0, 23.0), (9.0, 24.0), (9.2, 22.0), (14.8, 22.8), (16.0, 22.0),
(23.0, 23.0), (22.6, 19.0), (23.8, 17.8), (22.0, 14.0), (22.0, 11.0),
(24.0, 6.0), (23.0, 2.0), (19.0, 1.0), (16.0, 3.0), (10.0, 1.0), (11.0, 3.0),
(6.0, 2.0), (6.2, 3.0), (2.0, 3.0), (2.6, 6.2), (2.0, 8.0), (2.0, 11.0),
(5.0, 12.0), (2.0, 17.0), (3.0, 19.0), (6.0, 18.0), (6.5, 14.5),
(13.0, 19.0), (13.0, 12.0), (16.0, 8.0), (9.8, 8.0), (7.5, 6.0),
(12.0, 13.0), (19.0, 15.0)
]
boundary_nodes, points = convert_boundary_points_to_indices(curves; existing_points=points)
edges = Set(((1, 19), (19, 12), (46, 4), (45, 12)))
## Extract the x, y
tri = triangulate(points; boundary_nodes = boundary_nodes, segments = edges)
z = [(x - 1) * (y + 1) for (x, y) in DelaunayTriangulation.each_point(tri)] # note that each_point preserves the index order
f, ax, _ = tricontourf(tri, z, levels = 30; axis = (; aspect = 1))
f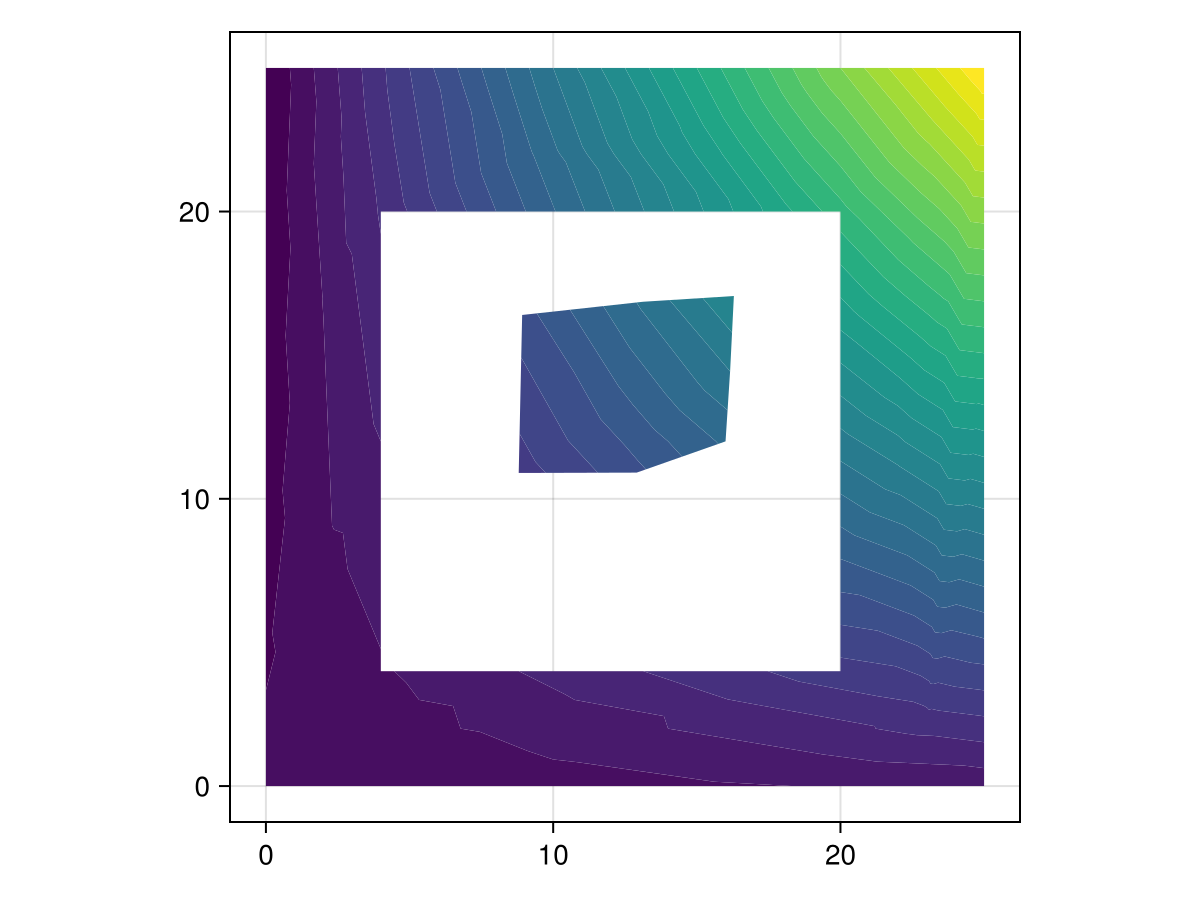
using CairoMakie
using DelaunayTriangulation
using Random
Random.seed!(1234)
θ = [LinRange(0, 2π * (1 - 1/19), 20); 0]
xy = Vector{Vector{Vector{NTuple{2,Float64}}}}()
cx = [0.0, 3.0]
for i in 1:2
push!(xy, [[(cx[i] + cos(θ), sin(θ)) for θ in θ]])
push!(xy, [[(cx[i] + 0.5cos(θ), 0.5sin(θ)) for θ in reverse(θ)]])
end
boundary_nodes, points = convert_boundary_points_to_indices(xy)
tri = triangulate(points; boundary_nodes=boundary_nodes)
z = [(x - 3/2)^2 + y^2 for (x, y) in DelaunayTriangulation.each_point(tri)] # note that each_point preserves the index order
f, ax, tr = tricontourf(tri, z, colormap = :matter)
f
Relative mode
Sometimes it's beneficial to drop one part of the range of values, usually towards the outer boundary. Rather than specifying the levels to include manually, you can set the mode attribute to :relative and specify the levels from 0 to 1, relative to the current minimum and maximum value.
using CairoMakie
using Random
Random.seed!(1234)
x = randn(50)
y = randn(50)
z = -sqrt.(x .^ 2 .+ y .^ 2) .+ 0.1 .* randn.()
f, ax, tr = tricontourf(x, y, z, mode = :relative, levels = 0.2:0.1:1)
scatter!(x, y, color = z, strokewidth = 1, strokecolor = :black)
Colorbar(f[1, 2], tr)
f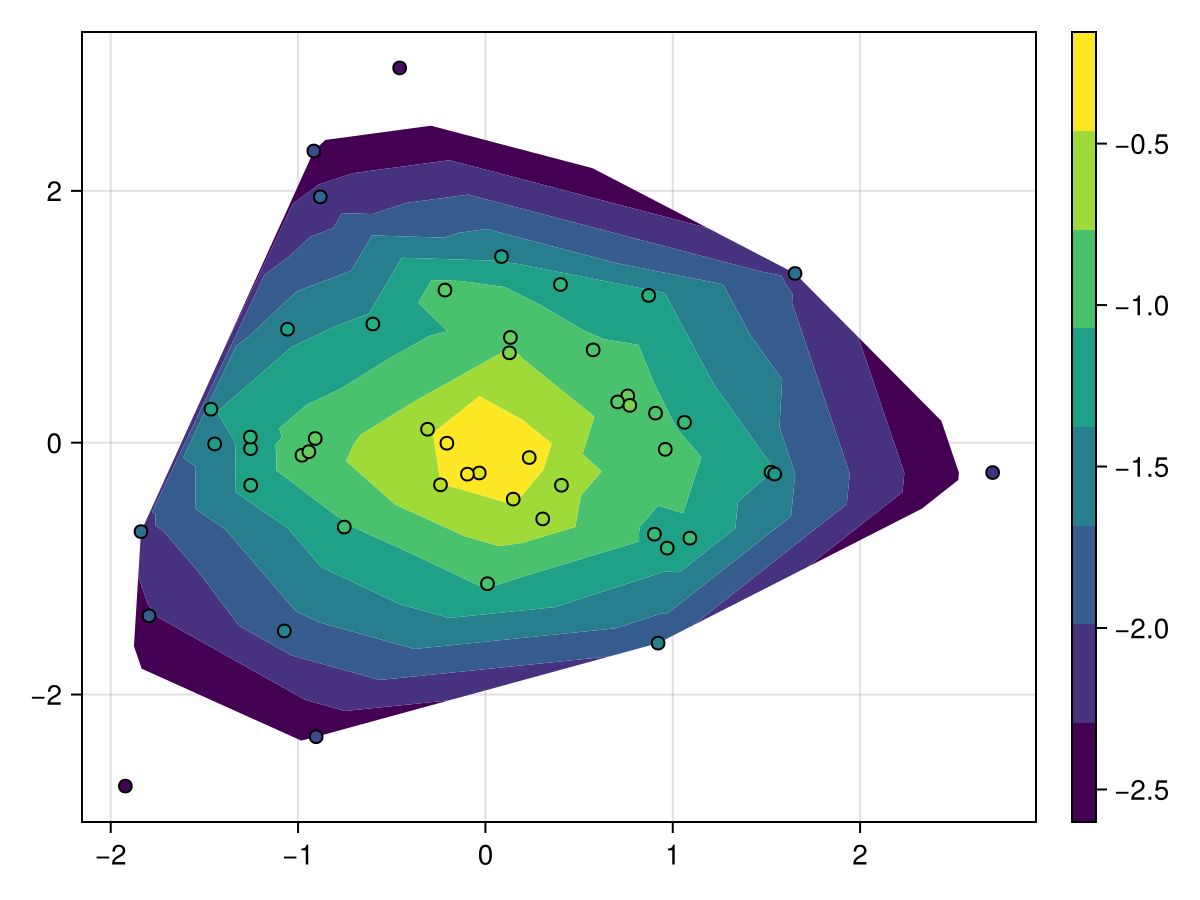
Attributes
alpha
Defaults to 1.0
The alpha value of the colormap or color attribute.
clip_planes
Defaults to @inherit clip_planes automatic
Clip planes offer a way to do clipping in 3D space. You can set a Vector of up to 8 Plane3f planes here, behind which plots will be clipped (i.e. become invisible). By default clip planes are inherited from the parent plot or scene. You can remove parent clip_planes by passing Plane3f[].
colormap
Defaults to @inherit colormap
Sets the colormap from which the band colors are sampled.
colorscale
Defaults to identity
Color transform function
depth_shift
Defaults to 0.0
Adjusts the depth value of a plot after all other transformations, i.e. in clip space, where -1 <= depth <= 1. This only applies to GLMakie and WGLMakie and can be used to adjust render order (like a tunable overdraw).
extendhigh
Defaults to nothing
This sets the color of an optional additional band from the highest value of levels to maximum(zs). If it's :auto, the high end of the colormap is picked and the remaining colors are shifted accordingly. If it's any color representation, this color is used. If it's nothing, no band is added.
extendlow
Defaults to nothing
This sets the color of an optional additional band from minimum(zs) to the lowest value in levels. If it's :auto, the lower end of the colormap is picked and the remaining colors are shifted accordingly. If it's any color representation, this color is used. If it's nothing, no band is added.
fxaa
Defaults to true
Adjusts whether the plot is rendered with fxaa (fast approximate anti-aliasing, GLMakie only). Note that some plots implement a better native anti-aliasing solution (scatter, text, lines). For them fxaa = true generally lowers quality. Plots that show smoothly interpolated data (e.g. image, surface) may also degrade in quality as fxaa = true can cause blurring.
inspectable
Defaults to @inherit inspectable
Sets whether this plot should be seen by DataInspector. The default depends on the theme of the parent scene.
inspector_clear
Defaults to automatic
Sets a callback function (inspector, plot) -> ... for cleaning up custom indicators in DataInspector.
inspector_hover
Defaults to automatic
Sets a callback function (inspector, plot, index) -> ... which replaces the default show_data methods.
inspector_label
Defaults to automatic
Sets a callback function (plot, index, position) -> string which replaces the default label generated by DataInspector.
levels
Defaults to 10
Can be either an Int which results in n bands delimited by n+1 equally spaced levels, or it can be an AbstractVector{<:Real} that lists n consecutive edges from low to high, which result in n-1 bands.
mode
Defaults to :normal
Sets the way in which a vector of levels is interpreted, if it's set to :relative, each number is interpreted as a fraction between the minimum and maximum values of zs. For example, levels = 0.1:0.1:1.0 would exclude the lower 10% of data.
model
Defaults to automatic
Sets a model matrix for the plot. This overrides adjustments made with translate!, rotate! and scale!.
nan_color
Defaults to :transparent
Sets the color used for nan values in the generated contour.
overdraw
Defaults to false
Controls if the plot will draw over other plots. This specifically means ignoring depth checks in GL backends
space
Defaults to :data
Sets the transformation space for box encompassing the plot. See Makie.spaces() for possible inputs.
ssao
Defaults to false
Adjusts whether the plot is rendered with ssao (screen space ambient occlusion). Note that this only makes sense in 3D plots and is only applicable with fxaa = true.
transformation
Defaults to :automatic
Controls the inheritance or directly sets the transformations of a plot. Transformations include the transform function and model matrix as generated by translate!(...), scale!(...) and rotate!(...). They can be set directly by passing a Transformation() object or inherited from the parent plot or scene. Inheritance options include:
:automatic: Inherit transformations if the parent and childspaceis compatible:inherit: Inherit transformations:inherit_model: Inherit only model transformations:inherit_transform_func: Inherit only the transform function:nothing: Inherit neither, fully disconnecting the child's transformations from the parent
Another option is to pass arguments to the transform!() function which then get applied to the plot. For example transformation = (:xz, 1.0) which rotates the xy plane to the xz plane and translates by 1.0. For this inheritance defaults to :automatic but can also be set through e.g. (:nothing, (:xz, 1.0)).
transparency
Defaults to false
Adjusts how the plot deals with transparency. In GLMakie transparency = true results in using Order Independent Transparency.
triangulation
Defaults to DelaunayTriangulation()
The mode with which the points in xs and ys are triangulated. Passing DelaunayTriangulation() performs a Delaunay triangulation. You can also pass a preexisting triangulation as an AbstractMatrix{<:Int} with size (3, n), where each column specifies the vertex indices of one triangle, or as a Triangulation from DelaunayTriangulation.jl.
visible
Defaults to true
Controls whether the plot gets rendered or not.