Transformations

Every plot and every scene contains a Transformation object which holds a transform_func and generates a model matrix.

Model Transformations

The model matrix is composed of a translation, scaling and rotation, with the rotation acting first and the translation acting last. The translation is set by translate!(), the scaling by scale!() and the rotation by rotate!(). Furthermore you can change the origin used for scaling and rotating with origin!().

using GLMakie
using GLMakie

box = Rect2f(0.9, -0.1, 0.2, 0.2)

f = Figure(size = (500, 450))
a = Axis(f[1, 1], aspect = DataAspect())
xlims!(a, 0.2, 1.2); a.xticks[] = 0.1:0.2:1.1
ylims!(a, -0.2, 0.8); a.yticks[] = -0.1:0.2:0.7

# Initial plot for reference
scatterlines!(a, box, color = 1:4, markersize = 20, linewidth = 5)

# Transformed plot
p2 = scatterlines!(a, box, color = 1:4, markersize = 20, linewidth = 5)
origin!(p2, 1,0,0) # apply rotation & scaling relative to the center of the box
scale!(p2, 2, 2)             # double x, y
Makie.rotate!(p2, pi/2)      # 90° rotation
translate!(p2, -0.5, 0.5)    # translate 0.5 left, 0.5 up

f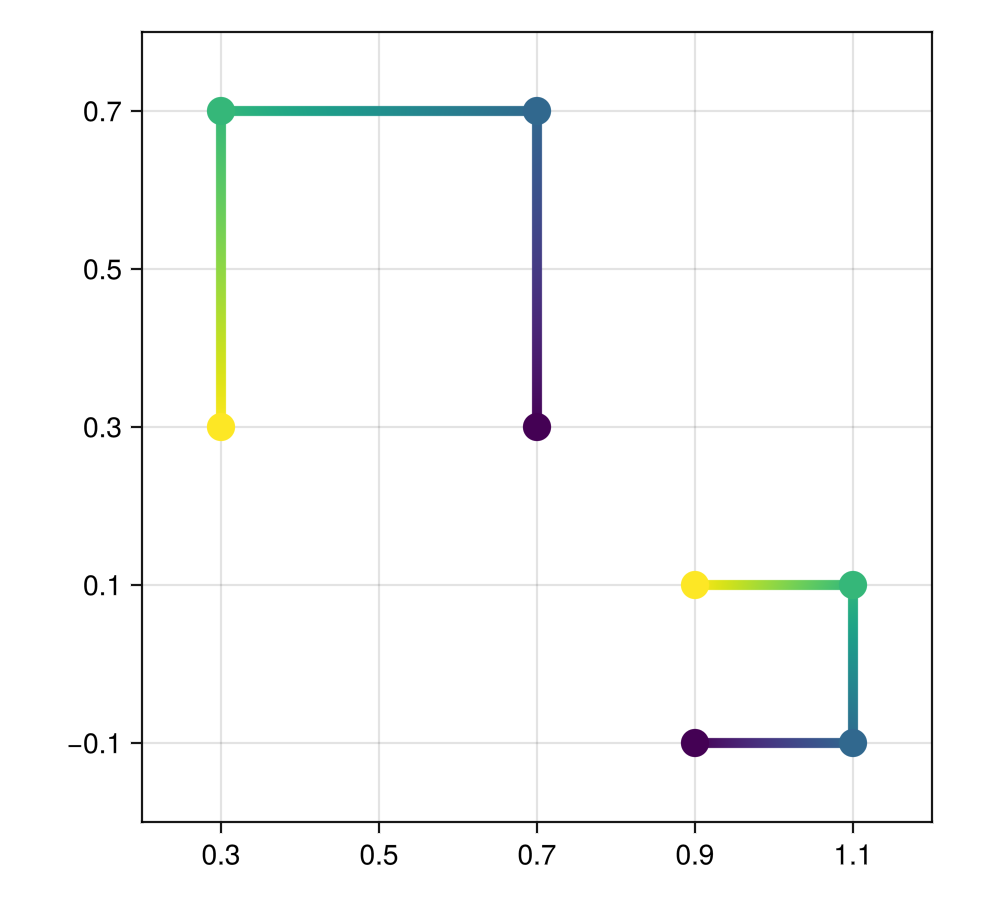

By default, calling these functions will overwrite the value set by a previous invocation. So if you call translate!(plot, 1,0,0); translate!(plot, 0,1,0) the translation will be (0,1,0). To accumulate transformation you need to add Accum as the first argument, e.g. translate!(Accum, plot, 0,1,0).

Transformation Function

The transform_func is a function that gets applied to the input data of a plot after convert_arguments() (type normalization) and dim_converts (handling of units and categorical value). It is typically managed by an Axis. For example, if you set ax.xscale[] = log, the underlying ax.scene will have it's transformation function set to (log, identity) which will propagate to the plots inside the axis/scene.

using Makie
f, a, p = scatter(1:10);
Makie.transform_func(a.scene) # (identity, identity)
Makie.transform_func(p) # (identity, identity)
a.xscale[] = log
Makie.transform_func(a.scene) # (log, identity)
Makie.transform_func(p) # (log, identity)

You can set the transformation function of a plot by updating plot.transformation.transform_func[] = new_func. This will also change the transformation function of each child plot. Note that this will usually be reset when the plots parent transformation function changes, e.g. if ax.xscale is set in the example above. You can avoid this by explicitly not inheriting the transformation function, or by constructing the Transformation object yourself. See below.

Scene Transformation

The Scene also holds onto a Transformation object. It doesn't affect the scene directly, but acts as a potential parent transformation to plots added to the scene. Whether it is used or not depends on the transformation attribute. By default it will be used if the space of the scene is compatible with the given plot.

transformation Attribute

The transformation attribute controls how the Transformation object is initialized. It is processed once during plot construction and then removed.

By default the attribute is set to Makie.automatic. In this case the transformation is inherited from the parent plot or scene if both use the same coordinate space. So if a parent scene uses a 3D camera and the plot uses space = :pixel, the transformation will not be inherited. If the camera is a pixel camera instead, it will be. When a transformation is inherited, the parent transform_func is reused and the parent model matrix acts as a secondary matrix transform. In Pseudocode we have:

transformation.model = parent.model * local_model
transformation.transform_func = parent.transform_func

Inheritance can be explicitly controlled with a couple of Symbols. For all of these the coordinate spaces of the parent and child are ignored.

• :inherit: Inherit both model and transform_func

• :inherit_model: Only inherit model

• :inherit_transform_func: Only inherit transform_func

• :nothing: Inherit neither making the new Transformation an identity transformation

The transformation attribute also accepts inputs to the transform!() function. This allows you to prepare a plot with an initial model transformation. You can pass scale, rotation and/or translation as part of a NamedTuple, Dict or Attributes, or rotate and translate the xy plane to another plane with (plane, shift). For example:

using CairoMakie
using CairoMakie

f = Figure()
# transform 0..1 Rect to -1..1 Rect
lines(f[1, 1], Rect2f(0, 0, 1, 1),
    transformation = (scale = Vec3f(2), translation = Vec3f(-1)))

a = LScene(f[1, 2])
heatmap!(a, rand(4,4), transformation = (:xy, 0.5))
heatmap!(a, rand(4,4), transformation = (:xz, 0.5))
heatmap!(a, rand(4,4), transformation = (:yz, 0.5))
f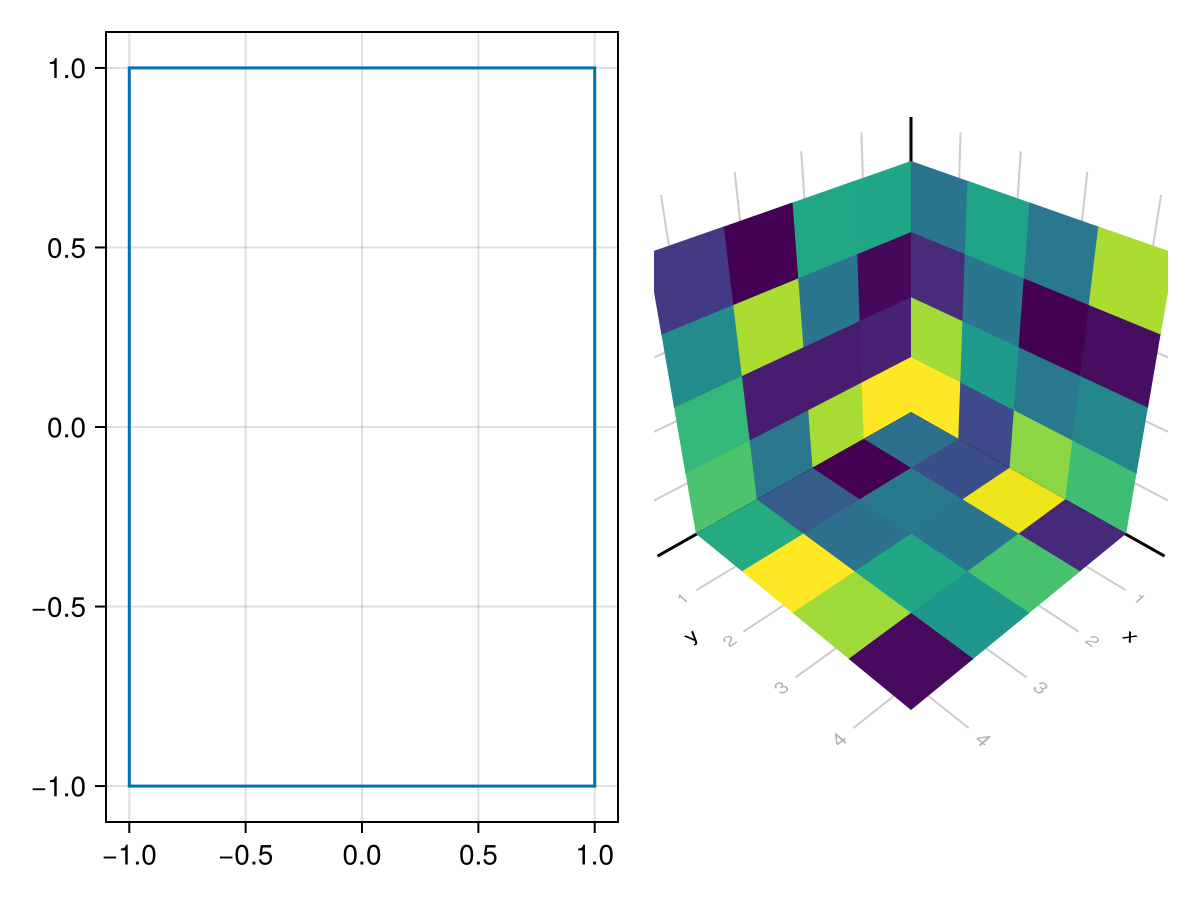

Finally you can also construct a Transformation object yourself and pass it through the transformation attribute.

Constructors

As eluded to in the transformation function section there are some cases where constructing a Transformation yourself can be useful. For example, you may want to apply transform_func before running a triangulation algorithm in a recipe so that the triangulation doesn't get distorted. Or you may want to chain transformations of a series of plots to keep them relative to each other (see below). There are a few constructors which are helpful to know for this.

If you want to fully detach a plot from its parents transformations, you can create it with transformation = Transformation(). If you want to remove only the transform_func but not model transformations, you can use transformation = Transformation(parent, transform_func = identity). You can also pass different starting values for translation, scale and rotation to these functions. This will not affect whether the parents model transformations are considered.

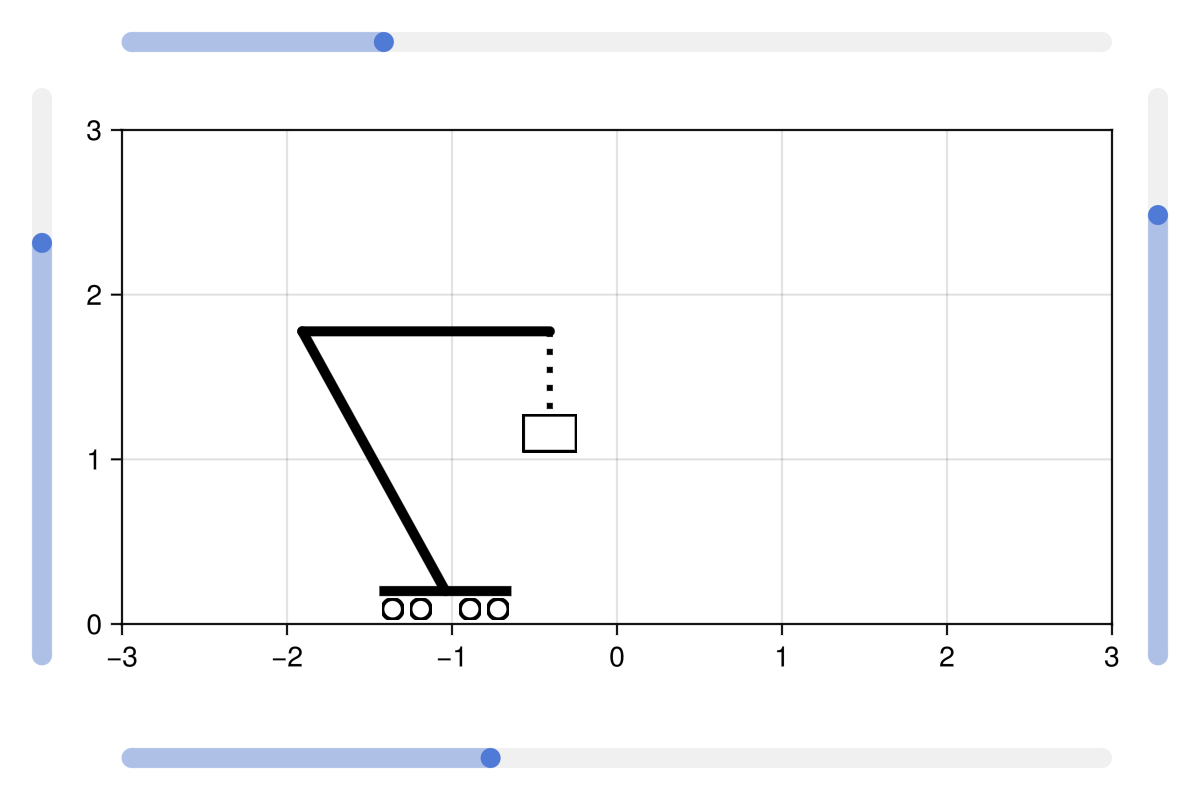
As an example, here are two arms on a cart raising a box with a rope.

using GLMakie
using GLMakie
using Makie: Vec3d

f = Figure(size = (600, 400))
a = Axis(f[2, 2], aspect = DataAspect())
ylims!(0, 3); xlims!(-3, 3)

# Cart
cart = Transformation()
scatter!(a, [-0.32, -0.15, 0.15, 0.32], fill(0.09, 4), transformation = cart,
    marker = Circle, color = :transparent, strokewidth = 2, strokecolor = :black,
    markerspace = :data, markersize = 0.1
)
linesegments!(a, [-0.4, 0.4], [0.2, 0.2], transformation = cart,
    color = :black, linewidth = 5
)

# arms
arm1 = Transformation(cart, origin = Vec3d(0, 0.2, 0))
linesegments!(a, [0, 0], [0.2, 2], transformation = arm1,
    color = :black, linewidth = 5, linecap = :round
)
arm2 = Transformation(arm1, origin = Vec3d(0, 2, 0))
linesegments!(a, [0.0, 1.5], [2, 2], transformation = arm2,
    color = :black, linewidth = 5, linecap = :round
)

# rope - we want this to just extend downwards rather than inherit rotations
rope_length = Observable(1.0)
rope_points = map(arm2.model, rope_length) do model, len
    # position of end of arm2 after transformations apply
    rope_origin = (model * Point4(1.5, 2, 0, 1))[Vec(1,2)]
    rope_end = rope_origin - Vec2(0, len)
    return [rope_origin, rope_end]
end
crate_origin = map(ps -> ps[2] .+ Vec2(0, -0.12), rope_points)

linesegments!(a, rope_points,
    color = :black, linewidth = 3, linestyle = :dot, linecap = :round
)
scatter!(a, crate_origin,
    marker = Rect, color = :white, strokewidth = 2, strokecolor = :black,
    markerspace = :data, markersize = Vec2f(0.3, 0.2)
)

# Move cart
sl1 = Slider(f[3, 2], range = range(-4, 4, length = 101))
on(v -> translate!(cart, v, 0, 0), sl1.value)
# Pivot arm 1
sl2 = Slider(f[1, 2], range = range(-pi/3, pi/3, length = 101))
on(v -> Makie.rotate!(arm1, -v), sl2.value)
# Pivot arm 2
sl3 = Slider(f[2, 1], range = range(-pi/3, pi/3, length = 101), horizontal = false)
on(v -> Makie.rotate!(arm2, -v), sl3.value)
# Extend rope
sl4 = Slider(f[2, 3], range = range(2, 0.1, length = 101), startvalue = 1.0, horizontal = false)
on(v -> rope_length[] = v, sl4.value)

# Set up some configuration
set_close_to!(sl1, -1.0) # move cart to -1
set_close_to!(sl2, -0.5) # angle arm1 to the left
set_close_to!(sl3, 0.5) # counter-angle arm2 to be horizontal
set_close_to!(sl4, 0.5) # raise crate

f