heatmap

heatmap(x, y, matrix)
heatmap(x, y, func)
heatmap(matrix)
heatmap(xvector, yvector, zvector)

Examples

Two vectors and a matrix

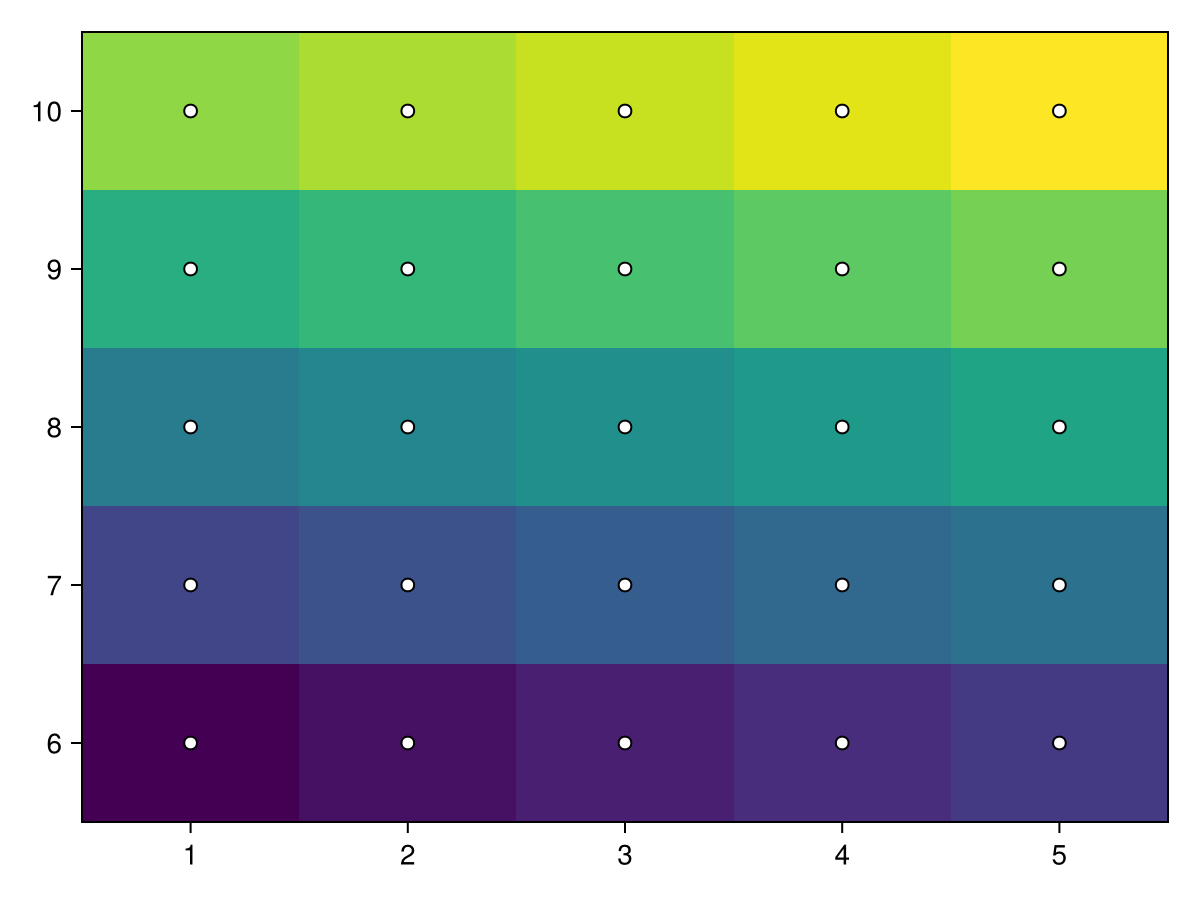
In this example, x and y specify the points around which the heatmap cells are placed.

using CairoMakie

f = Figure()
ax = Axis(f[1, 1])

centers_x = 1:5
centers_y = 6:10
data = reshape(1:25, 5, 5)

heatmap!(ax, centers_x, centers_y, data)

scatter!(ax, [(x, y) for x in centers_x for y in centers_y], color=:white, strokecolor=:black, strokewidth=1)

f

The same approach works for irregularly spaced cells. Note how the rectangles are not centered around the points, because the boundaries are between adjacent points like voronoi cells.

using CairoMakie

f = Figure()
ax = Axis(f[1, 1])

centers_x = [1, 2, 4, 7, 11]
centers_y = [6, 7, 9, 12, 16]
data = reshape(1:25, 5, 5)

heatmap!(ax, centers_x, centers_y, data)

scatter!(ax, [(x, y) for x in centers_x for y in centers_y], color=:white, strokecolor=:black, strokewidth=1)
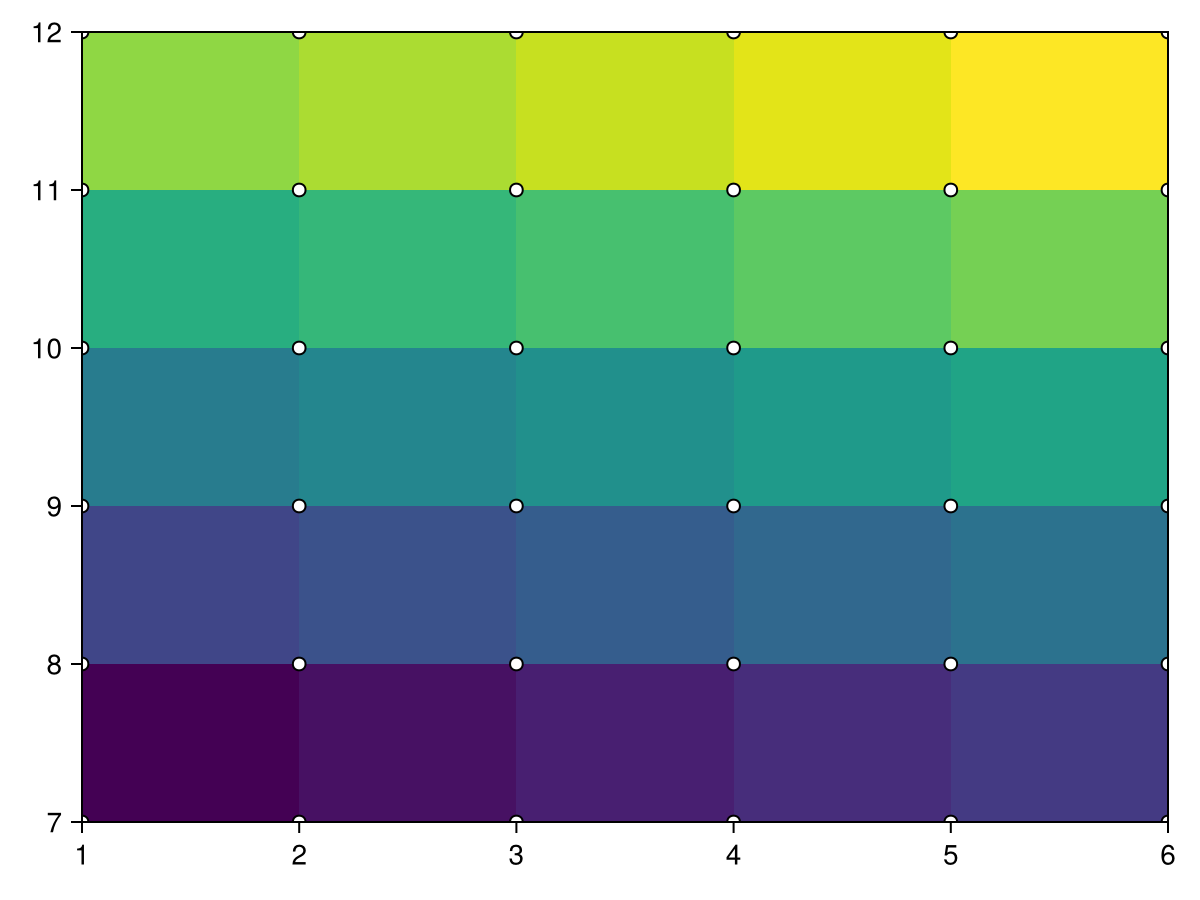
f

If we add one more element to x and y, they now specify the edges of the rectangular cells. Here's a regular grid:

using CairoMakie

f = Figure()
ax = Axis(f[1, 1])

edges_x = 1:6
edges_y = 7:12
data = reshape(1:25, 5, 5)

heatmap!(ax, edges_x, edges_y, data)

scatter!(ax, [(x, y) for x in edges_x for y in edges_y], color=:white, strokecolor=:black, strokewidth=1)
f

We can do the same with an irregular grid as well:

using CairoMakie

f = Figure()
ax = Axis(f[1, 1])

borders_x = [1, 2, 4, 7, 11, 16]
borders_y = [6, 7, 9, 12, 16, 21]
data = reshape(1:25, 5, 5)

heatmap!(ax, borders_x, borders_y, data)
scatter!(ax, [(x, y) for x in borders_x for y in borders_y], color=:white, strokecolor=:black, strokewidth=1)
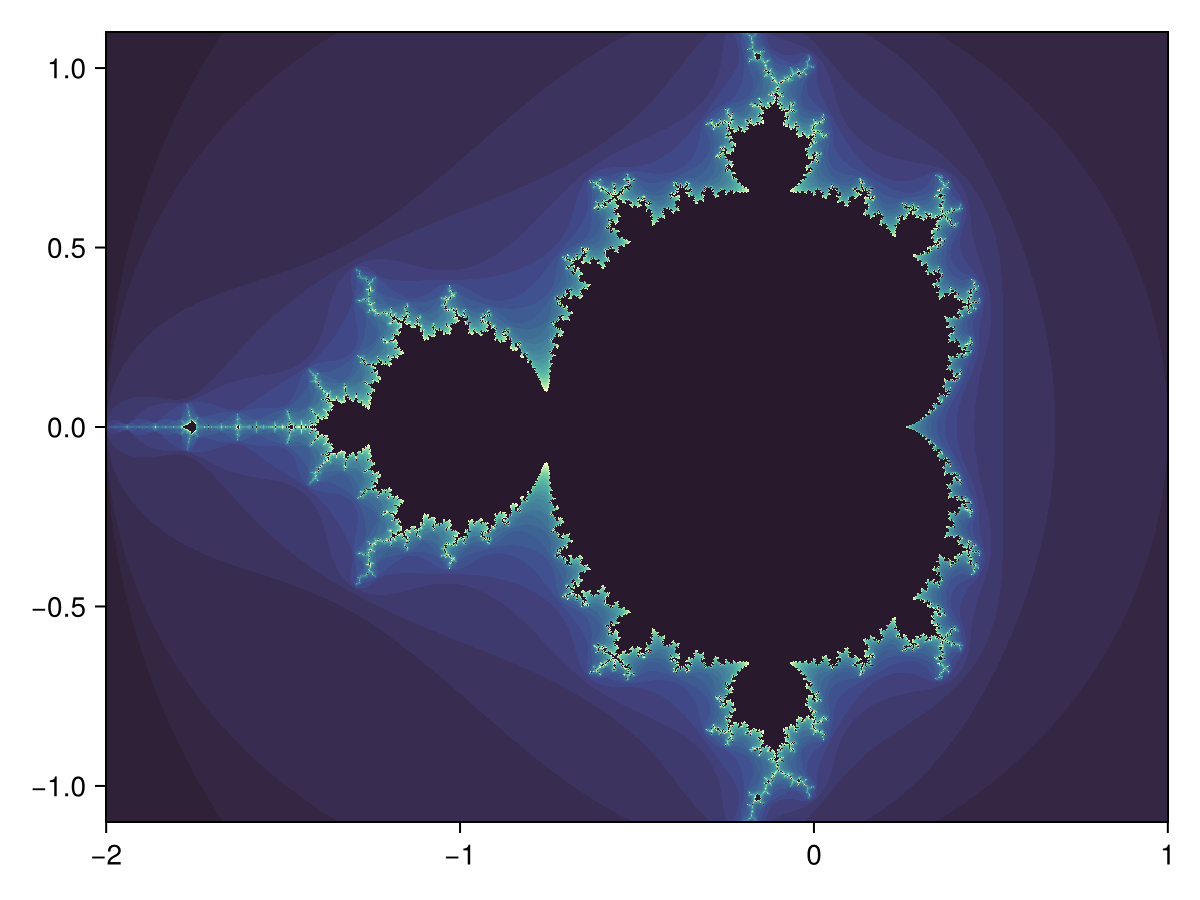
f

Using a Function instead of a Matrix

When using a Function of the form (i, j) -> v as the values argument, it is evaluated over the grid spanned by x and y.

using CairoMakie


function mandelbrot(x, y)
    z = c = x + y*im
    for i in 1:30.0; abs(z) > 2 && return i; z = z^2 + c; end; 0
end

heatmap(-2:0.001:1, -1.1:0.001:1.1, mandelbrot,
    colormap = Reverse(:deep))

Three vectors

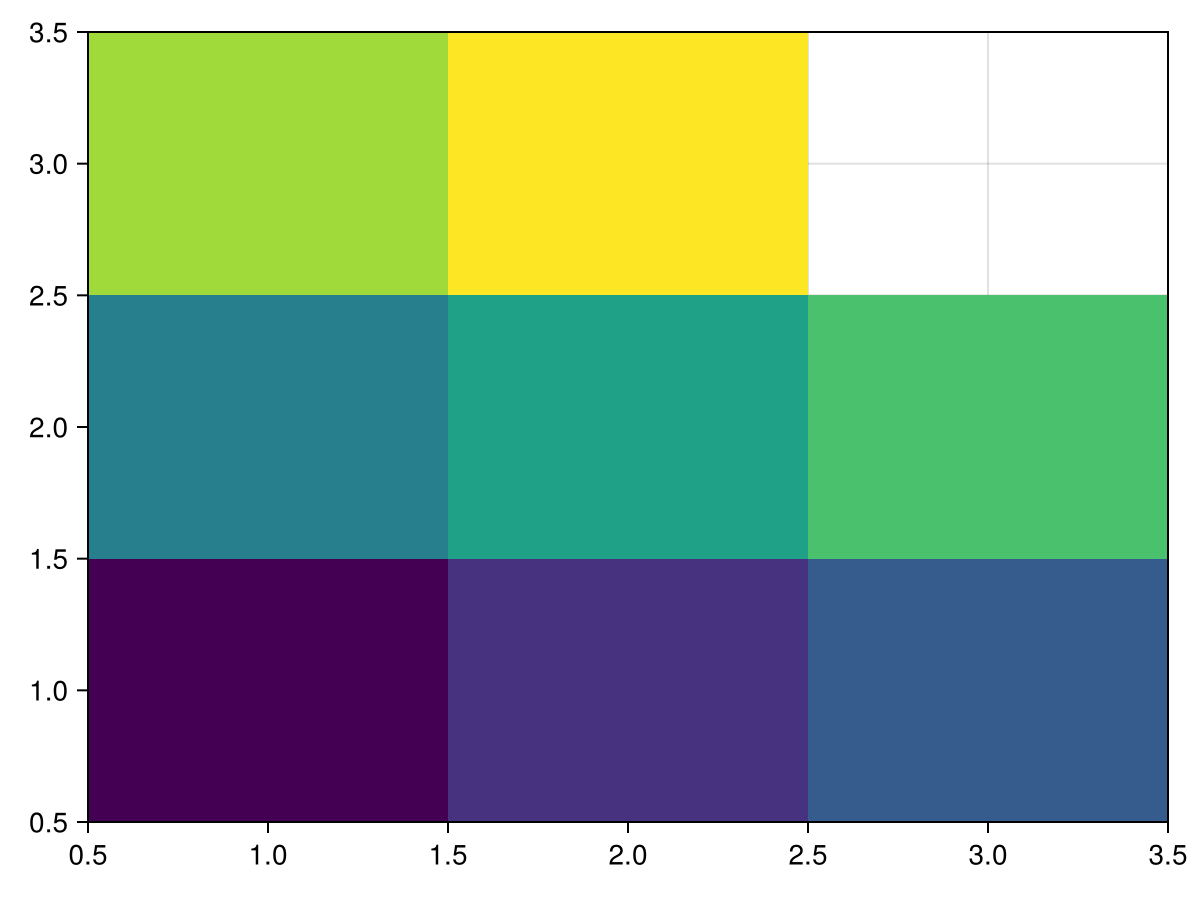
There must be no duplicate combinations of x and y, but it is allowed to leave out values.

using CairoMakie



xs = [1, 2, 3, 1, 2, 3, 1, 2, 3]
ys = [1, 1, 1, 2, 2, 2, 3, 3, 3]
zs = [1, 2, 3, 4, 5, 6, 7, 8, NaN]

heatmap(xs, ys, zs)

Colorbar for single heatmap

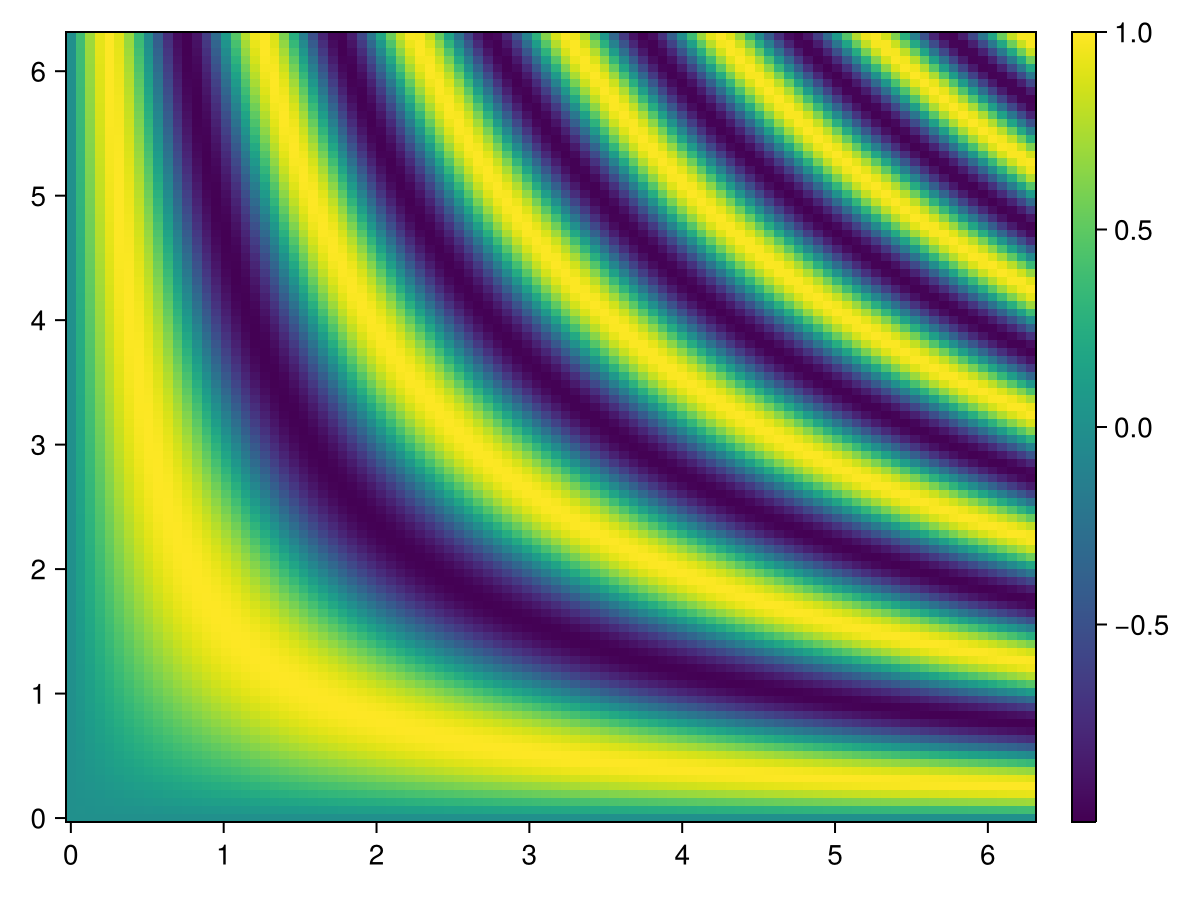
To get a scale for what the colors represent, add a colorbar. The colorbar is placed within the figure in the first argument, and the scale and colormap can be conveniently set by passing the relevant heatmap to it.

using CairoMakie


xs = range(0, 2π, length=100)
ys = range(0, 2π, length=100)
zs = [sin(x*y) for x in xs, y in ys]

fig, ax, hm = heatmap(xs, ys, zs)
Colorbar(fig[:, end+1], hm)

fig

Colorbar for multiple heatmaps

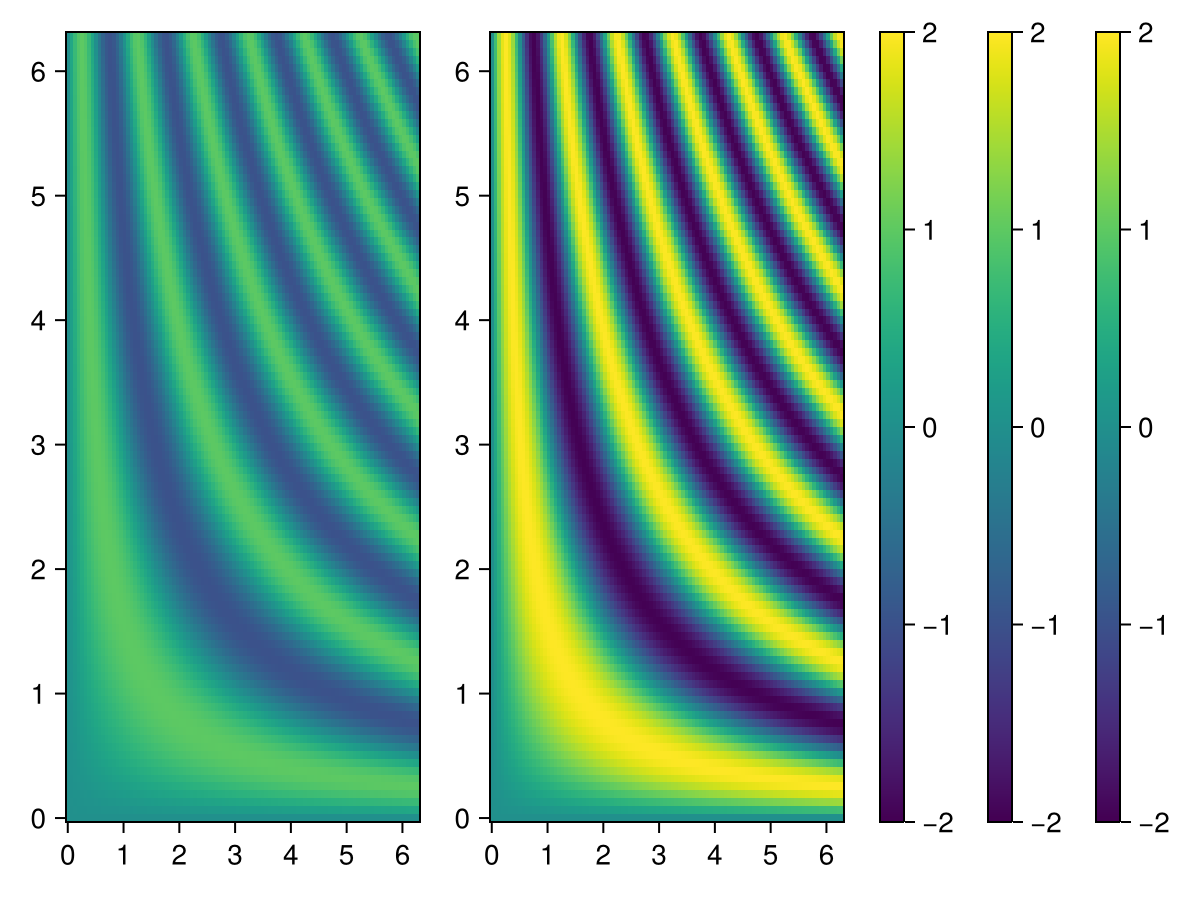
When there are several heatmaps in a single figure, it can be useful to have a single colorbar represent all of them. It is important to then have synchronized scales and colormaps for the heatmaps and colorbar. This is done by setting the colorrange explicitly, so that it is independent of the data shown by that particular heatmap.

Since the heatmaps in the example below have the same colorrange and colormap, any of them can be passed to Colorbar to give the colorbar the same attributes. Alternativly, the colorbar attributes can be set explicitly.

using CairoMakie


xs = range(0, 2π, length=100)
ys = range(0, 2π, length=100)
zs1 = [sin(x*y) for x in xs, y in ys]
zs2 = [2sin(x*y) for x in xs, y in ys]

joint_limits = (-2, 2)  # here we pick the limits manually for simplicity instead of computing them

fig, ax1, hm1 = heatmap(xs, ys, zs1,  colorrange = joint_limits)
ax2, hm2 = heatmap(fig[1, end+1], xs, ys, zs2, colorrange = joint_limits)

Colorbar(fig[:, end+1], hm1)                     # These three
Colorbar(fig[:, end+1], hm2)                     # colorbars are
Colorbar(fig[:, end+1], colorrange = joint_limits)  # equivalent

fig

Using a custom colorscale

One can define a custom (color)scale using the ReversibleScale type. When the transformation is simple enough (log, sqrt, ...), the inverse transform is automatically deduced.

using CairoMakie

x = 10.0.^(1:0.1:4)
y = 1.0:0.1:5.0
z = broadcast((x, y) -> x - 10, x, y')

scale = ReversibleScale(x -> asinh(x / 2) / log(10), x -> 2sinh(log(10) * x))
fig, ax, hm = heatmap(x, y, z; colorscale = scale, axis = (; xscale = scale))
Colorbar(fig[1, 2], hm)

fig